Проблема качества маркетинговых исследований стоит перед разработчиками рекламных стратегий достаточно остро и, как правило, сводится к соответствию получаемых в результате данных реальному положению дел. Однако мало кто задумывается над тем, что те цифры, на основе которых будут приниматься судьбоносные для рекламной кампании решения, не являются величинами абсолютными, и чтобы действительно ориентироваться в ситуации, опираясь на исследования, необходимо учитывать погрешность измерений. Предлагаемая автором методика позволяет подойти к статистике со всей серьезностью и научиться за цифрами видеть то, что недоступно невооруженному взгляду неспециалиста.
Маркетинг для России — сравнительно новая прикладная наука. Здесь, в основном, работают представители «смежных» профессий — социологи, психологи, экономисты и т.д.
Смешение профессиональных культур тормозит развитие собственной культуры проведения маркетинговых исследований (в дальнейшем — МИ) и представления их результатов, на основании которых заказчик исследований должен принимать решения и вести свой бизнес.
Рассмотрим частный вопрос о статистической погрешности количественных МИ и о том, как в связи с наличием данной погрешности целесообразно представлять результаты.
Проводя количественные (или статистические) измерения различных параметров рынка, исследователь получает конкретные результаты, выраженные в цифрах, — проценты, рейтинги и т.д. Данные цифры, оформленные в виде системы таблиц, графиков и т.п., сопровожденные выводами и рекомендациями, представляются заказчику.
Здесь есть одна проблема, скорее всего не известная заказчику, но о которой исследователь должен знать.
Все представленные в отчете цифры — есть только оценка измеряемого параметра, сделанная исследователем на основании проведенных статистических измерений. Оценка в принципе не точна, хотя бы потому, что имеет т.н. «статистическую погрешность» (в принципе данные могут иметь иные виды погрешности, например, связанные с ошибками исследователя при проектировании и организации самого процесса исследования, неправильной постановки задачи и т.д. Мы их здесь не рассматриваем).
Иными словами, предоставленные цифры имеют свои %.
Естественно, чем больше величины выборки статистических измерений, тем меньше статистическая погрешность.
Исследователь является профессионалом, поэтому, скорее всего, знает о величине статистической погрешности в представленных заказчику данных. Исследователь в отчете указывает, как правило, величину статистической погрешности.
Но заказчик может и не знать, что означает указанная исследователем в отчете статистическая погрешность, а главное, что с этой погрешностью делать, как ее учитывать при проектировании своей дальнейшей деятельности.
Ниже рассмотрим два основных вопроса:
- Статистические погрешности измерений. (В основном, для профессионалов).
- Как корректно представлять заказчику количественные данные при имеющейся статистической погрешности.
Пример. Фрагмент отчета по статистике заболеваемости населения Москвы.
Вопрос: «Вы болели гриппом последнее время?»
При проведении выборочного опроса ответы распределились следующим образом (в абсолютных цифрах):
| Болели гриппом в течение последних ... | Частота (чел.) |
| 2 недель | 43 |
| 1 месяца | 79 |
| 2 месяцев | 113 |
| 3 месяцев | 86 |
| полугода | 80 |
| Всего | 401 |
Величина статистических погрешностей
Допустим, мы хотим оценить некий параметр р рынка. С этой целью мы проводим статистическое измерение на выборке n.
Отметим, что число р есть абсолютно точное значение искомого параметра, которое нам неизвестно и не может быть известно в принципе, но которое нам надо оценить методом статистических измерений.
Доверительная вероятность и соответствующий ей интервал
Проводя статистическое измерение, мы можем получить оценку р* нашего искомого параметра р.
Наша оценка р* будет находиться где-то вблизи истинного значения параметра р, и, скорее всего, не будет точно равна р.
Распределение возможных значений оценок значения искомого параметра f(p*), подчиняется, в общем случае, нормальному (Гауссовому) закону — рис.1.
рис.1.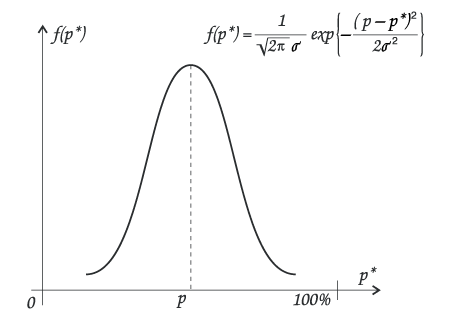
Здесь ![]() =3,14159...
=3,14159...
![]() — т.н. среднеквадратичное отклонение (СКО), величина, зависимая от объема выборки n: чем больше выборка, тем меньше отклонение.
— т.н. среднеквадратичное отклонение (СКО), величина, зависимая от объема выборки n: чем больше выборка, тем меньше отклонение.
Площадь, ограниченная гауссовой кривой и горизонтальной осью, равна 1.
Рассмотрим процент А% площади под кривой вблизи р в границах от р-х до р+х. (рис. 2)
рис.2.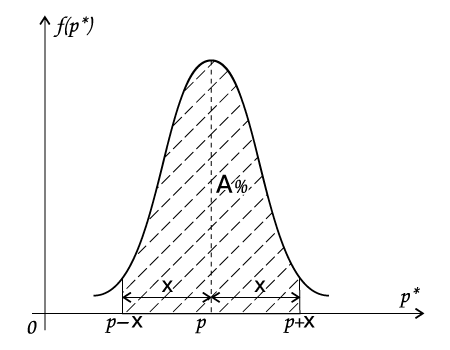
С вероятностью А% полученная оценка р* будет находиться в границах от р-х до р+х.
Вероятность А% называют доверительной вероятностью. Говорят: с вероятностью А% наша оценка р* будет находиться в интервале между нижней границей р-х и верхней границей р+х вблизи р.
Или сокращенно — «р%х».
Принята стандартная величина доверительной вероятности А=95%, в этом случае наш интервал будет иметь границы %2![]() вблизи р. Или — р%2
вблизи р. Или — р%2![]() (рис.3).
(рис.3).
рис.3.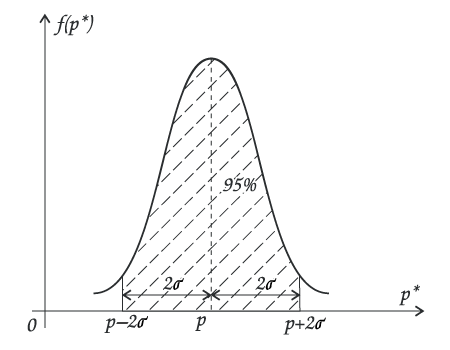
Правдоподобие
В предыдущем разделе вопрос стоял о том, где вблизи истинного значения параметра р может находиться наша оценка р*.
В жизни — наоборот. Мы не знаем истинного значения р, но, проведя статистические измерения, находим оценку р*.
Вопрос о погрешности нашей оценки ставится следующим образом: каков тот интервал вблизи р*, где может находиться (с вероятностью А%) истинное значение параметра р?
Иными словами, р% сколько? при данной выборке n.
Рассмотрим этот вопрос.
Итак, мы имеем оценку р*. Мы вправе выдвинуть гипотезу: «истинное значение параметра р есть р1 (рис. 4)», либо гипотезу: «истинное значение параметра р есть р2», либо «истинное значение параметра р есть р3», см рис.4.
рис.4.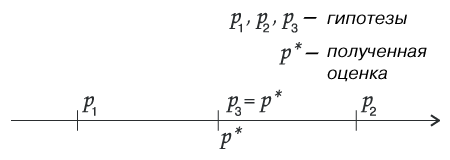
ПРАВДОПОДОБИЕ гипотезы относительно истинного значения параметра р равно условной вероятности того, что мы получим оценку р*, если на самом деле истинное значение параметра равно р.
Иными словами, мы предполагаем, что знаем параметр р (условие). И мы смотрим, какова условная вероятность появления оценки р*:
W(p* | p)
Реально значение р нам не известно. Мы предполагаем (выдвигаем гипотезу), что, допустим, оно равно р1. Напомню, мы, проведя статистические измерения, получили число р* в качестве оценки параметра р.
Условная вероятность при гипотетическом значении р1 появления нашей оценки р*, иными словами, правдоподобие гипотезы р1, иными словами, W(p* | p), есть — рис.5.
рис. 5.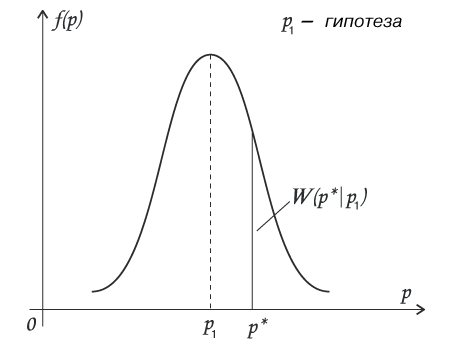
Строго говоря, вероятность есть площадь под кривой рис.5., поэтому вероятность получения данной конкретной оценки р* при гипотезе р1 есть бесконечно малое число.
Но это число все-таки меньше, чем вероятность получения нашей оценки р*, если мы примем гипотезу р3 = р*. (рис.6)
рис.6.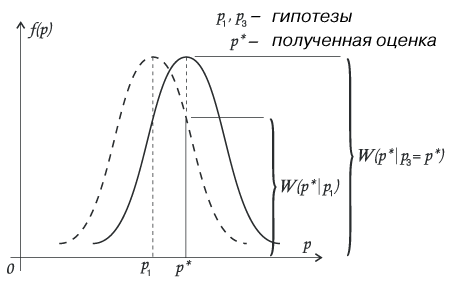
Удобно использовать отношение правдоподобий.
![]()
При условии, что в числителе и в знаменателе дроби бесконечно малые величины, отношение правдоподобий есть конкретная ненулевая величина, что делает отношение правдоподобий весьма практичным для решения многих задач.
В нашем случае наиболее правдоподобной будет гипотеза, что истинное значение параметра р равно нашей оценке р*. Однако весьма правдоподобной выглядит гипотеза, что истинное, но неизвестное нам, значение параметра р чуть больше, либо чуть меньше чем р*.
Нам необходимо:
- Найти численное значение границы отношения правдоподобий. Если отношение правдоподобий для данной гипотезы меньше этого числа, гипотеза считается достаточно правдоподобной, если больше — малоправдоподобной.
- На основании отношения правдоподобия определить интервал статистической погрешности оценки р* при данной выборке .
- Определим граничные значения отношения правдоподобия для стандартной доверительной вероятности А=95%. (рис.2)
Граничному отношению правдоподобия соответствуют границы интервала вблизи р*, (назовем их ргр), верхняя и нижняя, которые и определяют интервал статистической точности нашей оценки р*.
Граничное отношение правдоподобий
рис.7.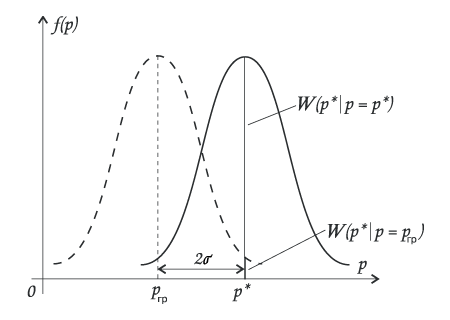
Правдоподобие при ргр: W(p* | p=ргр)
Граничное отношение правдоподобий (для А=95%):
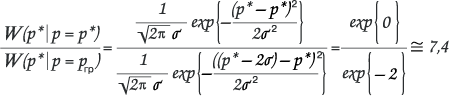
Итак, для интервала, в пределах которого, вблизи р*, в условиях доверительной вероятности А=95%, может находиться истинное значение параметра р, иными словами — для интервала погрешности статистических измерений характерно следующее правило:
На границах данного интервала отношение правдоподобий равно 7,4; внутри интервала — меньше, вне — больше, чем 7,4.
Вычисление интервалов погрешности
Объем выборки, напомню, n.
Предположим, r из них подходят под условия параметра.
Оценка р*:
![]() (1)
(1)
Если исследуемый параметр р достаточно большая величина, т.е. в пределах 5-95%, возможные значения оценок р* подчиняются биномиальному закону. Границы интервала статистической погрешности находим из уравнения:
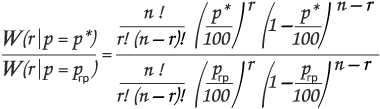
сокращаем:
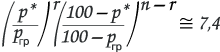
Решая уравнение численным методом, вычисляем границы интервалов статистической погрешности для каждого значения р*, лежащего в пределах 5-95%, для различных значений n.
Если исследуемый параметр р мал, лежит в пределах до 5%, то применим закон Пуассона:
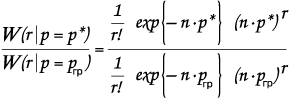
сокращаем:
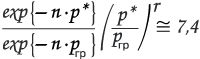
Результаты расчетов верхней и нижней границ интервалов статистической погрешности для различных значений оценок р* при разных выборках n представлены ниже в виде графиков на рис. 8.
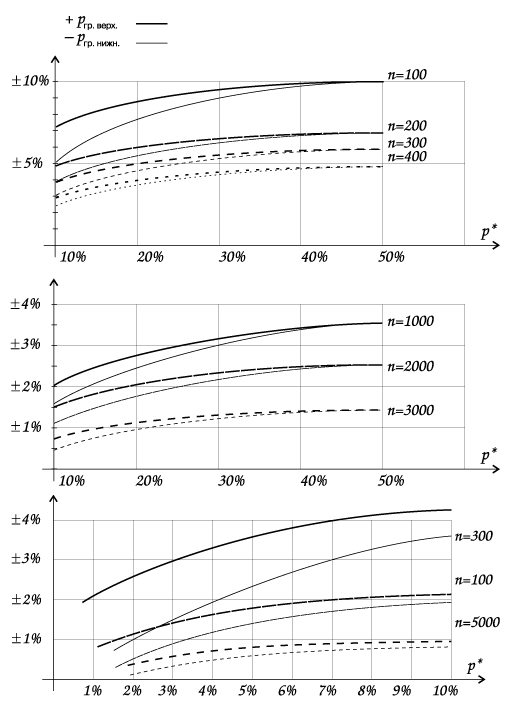
Основные комментарии
1. На графиках представлен интервал возможных значений р* от 0% до 50% для экономии места. Графики симметричны относительно линии 50%.
Погрешность оценки (верхняя и нижняя границы интервалов), скажем, для р*=60% равна погрешности (соответственно, нижней и верхней границ интервалов) оценки р*=40%.
2.Чем меньше оценка р*, тем меньше погрешность статистических измерений. Максимальная погрешность измерений будет при оценках в районе 50%. При дальнейшем увеличении значения оценки погрешность статистических измерений снова уменьшается.
3. Интервал погрешности несимметричен. Например, при объеме выборки n=100 и получившейся оценке параметра р*=30% интервал погрешности будет от 30—8% до 30+9%.
Пример. (продолжение)
В таблице, приведенной ранее, добавим столбцы, в которых:
- Результаты расчета относительной частоты приводимых ответов, выраженных в % по формуле (1), округленные до первой цифры после запятой.
- Границы интервала погрешности для каждой цифры (на основании графиков рис.8.).
- Величины интервала погрешности.
| Болели гриппом в течение последних ... | Частота (чел.) | Относительная частота (%) | Границы интервала погрешности (%) | Величина интервала погрешности (%) |
| 2 недель | 43 | 10,7 | от 8,2 до 13,7 | 5,5 (или +-2,3%) |
| 1 месяца | 79 | 19,7 | от 15,7 до 23,9 | 8,2 (или +-4,1%) |
| 2 месяцев | 113 | 28,2 | от 23,4 до 33,2 | 9,8 (или +-4,6%) |
| 3 месяцев | 86 | 21,4 | от 18,4 до 25,6 | 8,2 (или +-4,1%) |
| полугода | 80 | 20,0 | от 16,0 до 24,2 | 8,2 (или +-4,1%) |
| Всего | 401 | 100,0 |
Отметим следующие факты:
- Статистическая погрешность указанных измерений (с выборкой 401) такова, что может однозначно выявить различия между частотами ответов «2 недели», «1 месяц» и «2 месяца». Границы интервалов погрешности для указанных ответов не пересекаются.
- Статистическая погрешность измерений не может однозначно определить различий в частоте ответов «1 месяц», «3 месяца» и «полгода».
Иными словами, на основании представленных данных, можно сделать вывод что «тех, кто болел гриппом в последние 3 месяца больше, чем тех, кто болел гриппом в последний 1 месяц». Но этот вывод будет недостоверен.
Погрешность измерений и представление результатов
На практике часто случается, что объем выборки — не круглое число, при вычислении оценки параметра р* по формуле:
![]()
вполне может оказаться, что оценка р* будет не слишком «удобна»:
например:
n = 324
r = 103
р* = 31,790123... %
Как корректно округлить результат?
Рассмотрим, как задачу округления результатов решают инженеры.
Допустим, при измерении некого напряжения в некой сети, имеющийся вольтметр показал результат: 36,3 В
Однако любой прибор несовершенен, т.е. его показания неточны, имеют погрешности. Величина погрешности прибора обычно указывается в его паспорте и на панели.
Если наш вольтметр имеет погрешность +-1 В, то в протокол измерений инженер записывает цифру: 36 В
Таким образом, инженер округляет показания прибора до ближайшей 1, в соответствии с паспортной погрешностью прибора.
Иными словами, в протокол измерений записывается результат, округленный до последней достоверной цифры.
Погрешность прибора +-1 В, следовательно, десятки в цифре 36,3 достоверны, единицы — достоверны, а десятые доли вольта — недостоверны. Погрешность прибора не позволяет измерять десятые доли.
Поэтому десятые доли округляются до ближайшей 1 — в соответствии с арифметическими правилами округления.
Если бы вольтметр имел погрешность измерений +-0,5 В, то, получив результат 36,3 В, в протокол измерений мы должны занести 36,5 В.
Представлять в протоколе измерений только достоверные цифры — так понимается корректность работы с количественными данными любого типа.
Наш «прибор» — количественные статистические измерения. Погрешность нашего прибора зависит от объема выборки — см. рис. 8.
Профессиональная культура требует, чтобы в отчете представлялись только достоверные результаты:
Пример. (Продолжение)
Окончательный вид таблицы в отчете, с представлением математически корректных результатов:
| Болели гриппом в течение последних ... | Частота (чел.) | Относительная частота (%) | Величина интервала погрешности (%) |
| 2 недель | 43 | 10 | +-2,3% |
| 1 месяца | 79 | 20 | +-4,1% |
| 2 месяцев | 113 | 30 | +-4,6% |
| 3 месяцев | 86 | 20 | +-4,1% |
| полугода | 80 | 20 | +-4,1% |
| Всего | 401 | 100 |
Внимание! При округлении результатов следует иметь в виду: может получиться так, что сумма всех цифр не будет равна 100,0% (последняя строка в таблице).
Группа выводов 1
- При объеме выборки от 80 до 200 математически корректно округлять результаты статистических измерений до одного из следующих значений:
0%, 5%, 10%, 20% .... 80%, 90%, 95%, 100% - При объеме выборки 300-700 на участке оценок р* от 10% до 90% корректно округлять до ближайших 5%. На участках 0—10% и 90—100% до ближайших 3%.
- При объеме выборки 800-1500 на участках 10—90% округлять до ближайших 3%, на участках 0—10%, 90-100% — до ближайших 2%.
- При объеме выборки 2000-4000 на участке 10—90% — до ближайших 2%, на участке 0—10% и 90—100% — до ближайшего 1%.
- Только при объеме выборки свыше 5000 можно позволить на 10—90% округлять до 1%, на участках 0—10% и 90—100% — до ближайших 0,5%.
Группа выводов 2
- Если при проведении количественных измерений вас удовлетворяет точность +-10%, пользуйтесь объемом выборки 100: увеличение выборки вдвое ничего принципиально нового не принесет, кроме, разве что, увеличения бюджета.
- Аналогично и для требуемой точности +-5% вполне достаточно выборки около 350. Двукратное увеличение выборки не принесет существенных результатов.
- Для проведения прецизионных (особо точных) статистических измерений — с точностью до 0,1% — требуется выборка не менее 15-20 тыс.
- Если исследователь в отчете о количественных статистических измерениях указывает цифры с точностью до десятых долей %, и на основании десятых долей % делает некие выводы, то, скорее всего, он фальсифицирует их.
Представление математически корректных данных в отчете не избавляет от необходимости отдельно указывать статистическую погрешность проведенных статистических измерений.
Литература:
- Е.С. Вентцель. Теория вероятностей. Москва, 1962 г.
- В.С. Пугачев. Теория случайных функций и ее применения к задачам автоматического управления. Москва, 1960.
- Bierman H.J., Bonini C.P., Hausman W.H. Quantitative Analysis for Business Decisions. Irvin, 1991.
- Bowen E.K., Starr M.K., Basic Statistics for Business and Economics. McGraw-Hill, 1989.
Читайте также
А видел ли слона? Измерения эффективности медиа
Культура потребления. Черты российского потребителя

Комментарий
Новое сообщение