Факторный анализ (ФА) возник и начал развиваться в связи с необходимостью решения задач психологии. Его основоположником считается Ч. Спирмен, который в 1904 году в статье о природе интеллекта выдвинул предположение о существовании какого-либо фактора, общего для всех интеллектуальных тестов. В настоящее время область применения ФА значительно расширилась и охватывает многие разделы многомерного статистического анализа.
При проведении сегментирования факторный анализ используется прежде всего как метод сжатия данных, т. е. сокращения большого количества переменных. Переменные, которые могут быть использованы для сегментирования с применением кластерного анализа, сокращаются до некоторого основного набора составных переменных (факторов), которые затем и используются при кластеризации. Необходимость такого сокращения связана не только с желанием исследователя «ускорить» процедуру кластерного анализа, но и с некоторыми важными соображениями:
- если в кластерный анализ включаются несколько переменных, связанных с описанием одинаковых или близких характеристик (например, параметров товара), то эти характеристики получают гораздо больший вес. Поскольку расстояния вычисляются исходя из разностей между наблюдениями по каждой переменной, то несколько связанных переменных окажут большее влияние на результаты. Достаточно очевидной эта ситуация становится при рассмотрении гипотетического примера, когда в кластерном анализе участвуют две совершенно идентичные переменные. В этом случае двукратно усиливается воздействие измеряемой этими переменными характеристики на конечный результат. (Разумеется, на практике в опросный лист редко включаются совершенно идентичные вопросы, но близость измеряемых с помощью различных вопросов характеристик вполне возможна);
- важной причиной использования факторного анализа перед проведением кластеризации является четкость и простота интерпретации. Исследователю-маркетологу гораздо проще понять кластерное решение, основывающееся на анализе 5-6 факторов (если у них имеется осмысленная интерпретация), нежели решение для 50-60 переменных.
Таким образом, при наличии большого числа кластерных переменных сокращение данных с помощью методов факторного анализа часто может предшествовать кластеризации. Исследователь должен при этом четко представлять, что ФА относится к разведочным статистическим техникам и не может дать четких и однозначных ответов на все интересующие вопросы. Значительной остается роль исследователя при принятии решения о количестве факторов и их интерпретации — оно во многом основывается на знании предметной области, предшествующем опыте и интуиции.
Основные задачи при проведении ФА — это определение количества факторов и их интерпретация. Вообще для маркетолога интерпретируемость является одним из наиболее важных критериев при принятии решения о том, сохранять или удалять фактор, хотя с точки зрения математической статистики и метода ФА нет никакой необходимости в какой-либо интерпретации факторов. При подборе числа факторов пользуются различными статистическими показателями — собственными числами, долями объясненной дисперсии, но эти показатели также не являются абсолютно определяющими.
При изучении и сегментировании потребителей факторами обычно являются некоторые основные свойства товара или поведения потребителей, которые обнаруживаются с помощью ряда вопросов опросного листа. При проведении ФА прежде всего необходимо проанализировать корреляционную матрицу переменных, предназначенных для кластеризации. Искомые факторы должны быть линейно связаны с переменными:
(
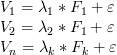
— переменные, 
— факторы, 
— нагрузки, 
— погрешность.)
Каждая переменная выражается через какой-либо фактор (), умноженный на коэффициент нагрузки (), плюс погрешность.
В этой системе уравнений неизвестными являются как , так и , а также погрешности . Поэтому приведенные факторные уравнения невозможно решить в их исходном виде. Но можно обратить внимание на то, что переменные коррелируют между собой (именно эта их особенность позволяет выразить все переменные через меньшее число факторов) и каждая из них содержит уникальную случайную компоненту или ошибку, которая не вносит никакого вклада в их корреляцию. Но в случае, когда переменные имеют общую компоненту, как, например, переменные V1 и V2 в приведенной выше системе уравнений имеют общий фактор F1, их корреляция связана с факторными нагрузками 
и 
. Применяя подобное рассуждение ко всем попарным корреляциям, можно оценивать коэффициенты нагрузки по корреляционной матрице — существующие подходы (метод наименьших квадратов, обобщенный метод наименьших квадратов, метод максимального правдоподобия) связаны с различными методами факторного анализа.
Таким образом, решить приведенную выше систему уравнений можно, только зная факторы Fi, для определения которых могут быть использованы две связанные между собой техники, объединенные общим термином «факторный анализ»:
- метод главных компонент;
- метод факторного анализа.
Метод главных компонент основан на попытке объяснить максимальную долю дисперсии в заданном наборе переменных и ориентируется на элементы на диагонали корреляционной матрицы (рис. 1), представляющие собой нормированные дисперсии. Метод факторного анализа пытается объяснить корреляции между переменными и, соответственно, больше сфокусирован на внедиагональных элементах корреляционной матрицы. Оба метода направлены на аппроксимацию корреляционной матрицы определенным числом факторов — меньшим, чем количество переменных, но способами аппроксимации они отличаются.
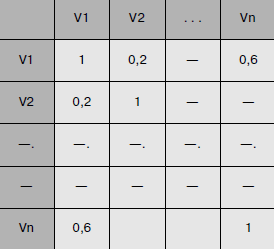
Рис. 1. Корреляционная матрица (пример)
Разумеется, методы дают схожие результаты: если главные компоненты объясняют большую часть дисперсии в переменных V1 и V2, они объясняют и почти всю корреляцию; в том случае, если факторы объясняют корреляцию между переменными V1 и V2, они также должны объяснять их дисперсию (пусть и не полностью).
Практические рекомендации по применению методов
Опыт практического применения методов показывает, что факторный анализ используется в том случае, когда исследователь заинтересован в изучении взаимосвязей между переменными, тогда как метод главных компонент применяют там, где исследователю больше необходимо именно сокращение размерности данных и меньше нужна их интерпретация. Тем не менее при обработке результатов маркетинговых исследований более популярным является метод главных компонент, поскольку им (в отличие от других факторных методов) можно пользоваться и при мультиколлинеарности данных. В опросных листах при проведении маркетинговых исследований, как правило, содержатся родственные вопросы, и полученные данные как раз и будут мультиколлинеарны. К тому же практика показывает, что для применения ФА необходимо иметь большое число наблюдений: оно должно быть как минимум на порядок больше числа выявленных факторов.
Существует ряд показателей, которые могут послужить исследователю ориентиром для предварительного выбора числа факторов или компонент. К наиболее важным относят собственные числа, значения которых в данном случае выражают долю дисперсии переменных, объясняемую данным фактором. Есть важное эмпирическое правило, полезное для оценивания числа факторов: имеется ровно столько факторов, сколько собственных чисел, больших 1. Это правило достаточно легко понять: собственное число выражает долю нормированной дисперсии переменных, объясняемую фактором, и если оно больше 1, то, следовательно, оно должно выражать дисперсию, содержащуюся более чем в одной переменной (максимальная доля нормированной дисперсии для одной переменной равна 1).
Необходимо еще раз подчеркнуть, что правило «единичного собственного числа» эмпирическое, вопрос о правомерности его применения должен решаться самим исследователем. Собственное число может быть меньше 1, но объяснять разброс, распределенный между несколькими переменными (например, собственное число, равное 0,9, объясняет по 1/3 разброса каждой из трех переменных). Для маркетолога при проведении сегментирования также очень важно, чтобы получаемые факторы имели содержательный смысл, поэтому факторы с собственными числами, большими 1, но не допускающими содержательной интерпретации, будут им отброшены, и, наоборот, могут быть оставлены факторы с собственными числами, меньшими 1.
Важным практическим вопросом, который необходимо решать при использовании метода факторного анализа, является вопрос вращений. Проще всего объяснить его на примере двухфакторного решения. Решение из двух факторов представляет собой двумерное пространство, которое определяется двумя осями, как это показано на рис. 2.
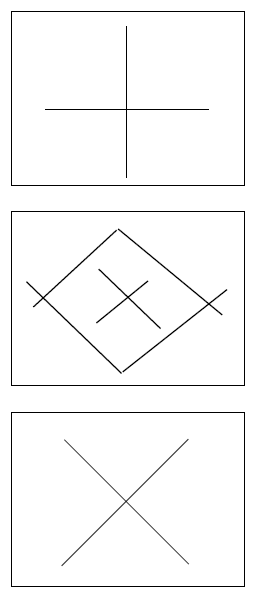
Рис. 2. Вращения в факторном анализе
Каждая пара осей определяет одно и то же двумерное пространство, но координаты точки в этом пространстве могут меняться в зависимости от используемой системы координат. Для метода главных компонент это не составляет никакой проблемы, поскольку он использует единственную ориентацию осей; в методе факторного анализа значения коэффициентов нагрузок меняются с изменением ориентации осей, а какой-либо определенной уникальной ориентации не существует. Эта трудность в использовании метода факторного анализа представляет собой фундаментальную математическую проблему. Для ее решения исследователь может применять различные эвристические методы, основой которых является нахождение такого вращения осей, которое максимизирует дисперсию коэффициентов нагрузок: некоторые нагрузки будут иметь большие значения, другие — маленькие. Такие вращения не позволяют однозначно, математически строго определять факторные нагрузки, но помогают исследователю упростить интерпретацию факторов, что очень важно при проведении сегментирования.
Существует несколько вариантов вращений. Самым популярным является метод варимакс, основанный на максимизации дисперсий переменных нагрузок на каждый фактор. Этот метод позволяет найти вращение, в результате которого одни переменные будут иметь высокие, а другие — низкие нагрузки на каждый фактор, что облегчает понимание и интерпретацию факторов. Метод вращения квартимакс позволяет найти такой поворот, при котором факторы для каждой переменной имеют и высокие, и низкие нагрузки. Метод вращения эквимакс представляет собой некоторый компромисс между первыми двумя методами. Все перечисленные выше вращения являются ортогональными (оси взаимно перпендикулярны), и, соответственно, будет наблюдаться отсутствие корреляции между факторами. Это очень важно для маркетолога, поскольку он может делать определенные заключения относительно независимых факторов. Существуют также и неортогональные вращения (оси не являются взаимно перпендикулярными), один из самых популярных методов — это облимин. Подобные вращения редко используются маркетологами, поскольку основной смысл проведения факторного анализа в данном случае заключается в получении относительно независимых составных показателей, когда факторы практически не коррелированы.
Метод главных компонент формально не требует использования вращений, так как предлагает единственное решение; но в практике исследователей-маркетологов обычно используется вращение варимакс для облегчения интерпретации компонент.
В том случае, когда результаты применения метода факторного анализа или метода главных компонент устраивают маркетолога, он может использовать в дальнейших исследованиях новый набор переменных, представляющих вклад каждого наблюдения в значение фактора. Новые переменные вычисляются умножением исходных переменных на набор весовых коэффициентов, полученных из коэффициентов нагрузок. Именно эти факторизованные переменные и могут быть использованы для проведения сегментирования. Как правило, эти переменные нормируют, сводя к переменным с нулевым средним значениям и единичным стандартным отклонениям.
Иногда специалисты используют коэффициенты нагрузок, чтобы узнать, какие переменные сильно связаны с фактором, а далее вычисляют новую переменную, которая является суммой или средним значением этого набора переменных. Это позволяет сохранять новые наблюдения в том же масштабе, что и исходные (при использовании средних значений) и таким образом обеспечить более понятную интерпретацию результатов.
Важной рекомендацией для использования метода факторного анализа является объем выборки. Как показывает опыт специалистов, число наблюдений должно быть достаточно велико и в 10-25 раз превышать число переменных, участвующих в факторном анализе. Это правило является эмпирическим, т. е. представляет собой сугубо практическую рекомендацию, и может быть объяснено тем, что факторный анализ основывается на корреляциях и для p переменных имеется p*(p-1)/2 возможных корреляций. Это правило не всегда соблюдается, технически при наличии p переменных для проведения факторного анализа достаточно p+1 наблюдений, но его соблюдение маркетологом очень желательно для получения более осмысленных результатов. В том случае, когда объем выборки мал по сравнению с числом переменных, маркетолог должен обратиться к методу главных компонент.
Существует несколько конкретных методов факторного анализа, наиболее распространенные из них различаются подходом к подгонке корреляционной матрицы. «Традиционным» методом является метод главных осей (метод PAF). Более современный — факторный анализ максимального правдоподобия; но если данные плохо обусловлены (например, почти мультиколлинеарны), метод максимального правдоподобия может выдавать не слишком осмысленные решения. В большинстве случаев результаты, полученные с помощью обоих методов, будут достаточно близкими, но если исследователь-маркетолог сомневается в обусловленности данных, предпочтительнее использовать более надежный метод главных осей.
Другие факторные методы менее популярны: к наиболее известным из них относится метод Q-факторного анализа, основанный на транспонировании матрицы данных и последующем проведении факторного анализа на респондентах вместо переменных. В этом случае корреляции вычисляются для каждой пары объектов на основании их откликов на переменные. На сегодняшний день этот метод в некоторой степени устарел, поскольку были созданы методы, более соответствующие подобной структуре данных (кластерный анализ).
Таким образом, при проведении сегментирования рынка обычно применяется метод главных компонент (вследствие мультиколлинеарности данных маркетинговых исследований) и для упрощения интерпретации результатов используется вращение варимакс. Если маркетолог уверен в отсутствии большого количества сильно коррелированных переменных (или других источников появления плохо обусловленных данных), то он может помимо метода главных компонент использовать также и факторный метод максимального правдоподобия. При этом всегда необходимо иметь в виду, что последний может привести к некорректному решению, если данные не являются хорошо обусловленными.
Читайте также
Культура потребления. Черты российского потребителя
Маска, я тебя знаю! Социально-демографические характеристики абонентов сотовой связи
Комментарий
23.05.2009 22:32
простое и понятное изложение
14.04.2010 10:25
Все просто и красиво
Новое сообщение