Дискриминантный анализ можно отнести к группе методов сегментирования, связанных с реакцией потребителя или откликом. Сегментирование, основанное на откликах, предполагает поиск таких сегментов, в которые попадут потребители, с наибольшей вероятностью предпринимающие определенные, предпочтительные для маркетолога действия (например, самое желанное действие - покупку товара, да еще и неоднократную). В связи с этим, в проводимом анализе используется некоторый критерий или решающее правило (связанное с принятием решения потребителем), что требует применения методов, отличных от кластерного анализа. К наиболее известным методам, используемым в подобных случаях, когда переменные сегментирования измерены в интервальной шкале, относятся дискриминантный анализ и логистическая регрессия.
Главной особенностью методов сегментирования, основанных на откликах, является такое формирование сегментов, при котором имеется явно заданный выходной критерий, и основная задача — максимизация этого критерия. В данном случае маркетолог определяет не естественные группы покупателей (как это делалось в методах, описанных в предыдущих статьях), а сегменты с такими потребителями, которые наиболее вероятно предпримут определенные действия. Как уже упоминалось выше, обычно (хотя и совсем не обязательно) под такими действиями понимается решение о покупке.
Можно заметить, что в данном случае исследователь производит поиск потребителей с характеристиками, предсказывающими их желательные действия. Математическая статистика предлагает ряд методов, подразумевающих категориальную природу выходного критерия: дискриминантный анализ, логистическая регрессия, логлинейное моделирование, построение деревьев классификации (например, CHAID-анализ). Каждый из этих методов предлагает различный способ оценки предсказывающих переменных (предикторов), определяющих желаемый отклик. Помимо предикторов исследователь должен определить также выходную (зависимую) переменную, в качестве которой может выступать какое-либо действие потребителя (например, предполагаемое приобретение товара).
На основании природы предсказывающих переменных, упомянутые выше методы можно разделить на две группы. Дискриминантный анализ и логистическая регрессия предполагают, что предикторы измерены по интервальной шкале [1], а логлинейные модели и алгоритмы построения деревьев классификации предполагают, что переменные являются категориальными или дискретными. Автор предполагает, прежде всего, рассмотреть методы дискриминантного анализа и логистической регрессии; логлинейные методы не рассматриваются из-за реальных проблем, возникающих при их использовании для сегментирования (в частности, требуется очень большое количество данных); алгоритмы построения деревьев классификации могут быть рассмотрены отдельно.
Метод дискриминантного анализа впервые был применен в сфере банковской деятельности, а именно — в кредитном анализе. Здесь наиболее четко прослеживается основной подход метода, подразумевающий привлечение прошлого опыта: необходимо определить, чем отличаются заемщики, вернувшие в срок кредит, от тех, кто этого не сделал. Полученная информация должна быть использована при решении судьбы новых заемщиков. Иначе говоря, применение метода имеет цель: построение модели, предсказывающей, к какой из групп относятся данные потребители, исходя из набора предсказывающих переменных (предикторов), измеренных в интервальной шкале. Дискриминатный анализ связан со строгими предположениями относительно предикторов: для каждой группы они должны иметь многомерное нормальное распределение с идентичными ковариационными матрицами [2].
Основные положения дискриминантного анализа легко понять из представления исследуемой области, как состоящей из отдельных совокупностей, каждая из которых характеризуется переменными с многомерным нормальным распределением. Дискриминантный анализ пытается найти линейные комбинации таких показателей, которые наилучшим образом разделяют представленные совокупности (рис. 1).
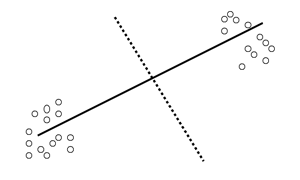
Рис. 1. Пример двух нормальных выборок с дискриминантной прямой
В данном примере две совокупности наилучшим образом разделяются с помощью прямой (называемой дискриминантной функцией), средняя точка между совокупностями является пороговым значением. Дискриминантная функция и пороговое значение могут быть использованы для классификации будущих наблюдений.
При использовании метода дискриминантного анализа главным показателем является точность классификации, и этот показатель можно легко определить, оценив долю правильно классифицированных при помощи прогностического уравнения наблюдений. Если исследователь работает с достаточно большой выборкой, применяется следующий подход: выполняется анализ по части данных (например, по половине), а затем прогностическое уравнение применяется для классификации наблюдений во второй половине данных. Точность прогноза оценивается, т.е. происходит перекрестная верификация. Поскольку маркетолог располагает, как правило, большим количеством предсказывающих переменных, он должен принять решение о том, какие из них будут использоваться в прогностическом уравнении. В дискриминантном анализе существуют методы пошагового отбора переменных, помогающие осуществить выбор предсказывающих переменных. Исследователь-маркетолог может (для переменных, фактически используемых в дискриминантной модели) оценить нормированные коэффициенты и использовать их как критерий относительной важности этих переменных.
Итак, целью дискриминантного анализа является получение прогностического уравнения, которое можно будет использовать для предсказания будущего поведения потребителей. Например, в отношении клиентов банка существует необходимость на основе некоторого набора переменных (возраст, годовой доход, семейное положение и т.п.) уметь относить их к одной из нескольких взаимоисключающих групп с большими или меньшими рисками не возврата кредита. Исследователь располагает некоторыми статистическими данными (значениями переменных) в отношении лиц, принадлежность которых к определенной группе уже известна. В примере с банком эти данные будут содержать статистику по уже предоставленным кредитам с информацией о том, вернул ли заемщик кредит или нет. Необходимо определить переменные, которые имеют существенное значение для разделения наблюдений на группы, и разработать алгоритм для отнесения новых клиентов к той или иной группе.
Метод дискриминантного анализа, как и вся группа методов, основанных на наблюдениях, предполагает использование определенной терминологии. Классифицируются объекты, а различные группы, к которым необходимо эти объекты относить, чаще всего называются классами. Алгоритм отнесения объектов к разным классам называется решающим правилом. Выборка, по элементам которой производится поиск решающего правила, называется обучающей, а в том случае, когда выборка делится на две части, по одной из которых строят решающее правило (обучающая), а по второй проверяют качество работы этого правила. Вторая выборка называется контрольной. Переменная, задающая принадлежность к классам, называется откликом, а остальные переменные, по которым строится обучающее правило, часто называют независимыми или предикторами.
Наиболее наглядно идея линейного дискриминантного анализа может быть объяснена для случая двух классов. Предположим, что имеется n-мерное пространство (n-количество предикторов), в котором каждый элемент выборки представлен точкой x. Два класса можно представить себе как два кластера точек, которые каким-либо образом разделены — в противном случае их невозможно было бы различать только по значениям предикторов. Требуется построить в пространстве границу более простой формы так, чтобы как можно больше точек одного класса лежало по одну сторону границы, а как можно больше точек другого класса — по другую сторону. В n-мерном пространстве речь идет о поиске гиперплоскости, которая наилучшим образом разделяла бы классы, или о поиске линейной комбинации вида:
(1) ![]()
Решающее правило может быть сформулировано следующим образом: если для данного объекта x выполнено неравенство F(x) > 0, он относится к первому классу;
если F(x) < 0 — ко второму классу.
Важной задачей является выбор способа оценки коэффициентов, позволяющий говорить об оптимальности решающего правила. Решающее правило можно назвать оптимальным, если по нему достигается минимальная вероятность ошибки. Линейные комбинации, удовлетворяющие условию оптимальности, называются (линейными) дискриминантными функциями. В математической статистике показано, что если каждый класс представляет собой выборку из многомерной нормальной совокупности, а все ковариационные матрицы классов равны между собой, то дискриминантный анализ оказывается оптимальным в том смысле, что никакой другой метод не позволяет добиться меньшей вероятности ошибки.
Итак, последовательность действий при применении метода дискриминантного анализа должна быть следующей:
- исследователь должен выбрать группирующую переменную с взаимоисключающими значениями. Объект может относиться только к одной из групп;
- исследователь определяет набор предикторов. Это решение очень важно для успешного проведения дискриминантного анализа;
- необходимо проверить, удовлетворяют ли имеющиеся данные всем предположениям, необходимым для проведения дискриминантного анализа (перечисление этих предположений дается ниже). Исследователь должен выделить выбросы, принять решение по отбрасыванию переменных, которые заведомо не могут быть хорошими предикторами;
- выбирается метод оценки параметров, задаются априорные вероятности для групп. Проверяется значимость различий средних по группам для каждой найденной функции; вычисляется относительная «важность» каждой функции, которая оценивается в терминах доли объясненной дисперсии. Здесь уже, разумеется, используются возможности соответствующих процедур SPSS;
- исследователь изучает полученные результаты классификации, принимает решение по поводу возможного расширения (или наоборот сужения) набора предикторов. Отдельно рассматриваются неверно классифицированные наблюдения, которые могут образовывать незамеченную ранее группу;
- специалисты рекомендуют на последнем шаге проверить качество построенного решающего правила, даже если исследователь-маркетолог полностью удовлетворен полученными результатами.
Итак, основой дискриминантного анализа является построение дискриминантных функций вида (1). Если имеется достаточное количество предикторов, число функций будет на единицу меньше числа групп, при поиске каждой из последующих функций требуется, чтобы отсутствовала ее корреляция со всеми предыдущими. Если, например, решается задача с тремя классами, строятся две дискриминантные функции.
Известны три основных подхода, связанных с отнесением объектов к различным классам по значениям дискриминантных функций:
- линейные классификаторы. Строятся k линейных функций и объект относится к k-тому классу, если значение k-й функции на нем оказывается максимальным [3];
- методы максимального правдоподобия (или вероятностные). Объект относится к классу k, если соответствующая апостериорная вероятность этой принадлежности максимальна. Применяемые в этих методах линейные дискриминантные функции часто называют каноническими;
- методы, связанные с расстояниями. Эта группа методов основана на подходе, связанном с отнесением объекта к тому классу, расстояние до центра которого является минимальным. Как правило, используется так называемое расстояние Махалонобиса.
В случае применения по умолчанию методов максимального правдоподобия (как, например, в SPSS) используются два набора оценок:
- априорные вероятности принадлежности к классу, которые можно рассматривать как решающее правило, применяемое в том случае, когда нет никакой дополнительной информации об объектах. Они вычисляются либо по числу объектов каждого класса, либо считаются равными друг другу (если имеется 5 классов, априорные вероятности будут равны 0,2);
- условные вероятности принадлежности к классу, каждая из которых равна вероятности получить соответствующее значение дискриминантной функции при условии, что объект принадлежит классу. Используется предположение о том, что значения дискриминантных функций распределены нормально.
Эти оценки позволяют применить формулу Байеса для вычисления апостериорных вероятностей принадлежности к классам. Именно эти вероятности и используются в решающем правиле: объект относится к тому классу, для которого эта вероятность максимальна.
В соответствии с правилом Байеса, вероятность того, что наблюдение с дискриминантным индикатором D принадлежит к группе i , оценивается соотношением:
![]()
P(Gi) — априорная вероятность принадлежности наблюдения к группе Gi, представляющая собой оценку вероятности при условии, что отсутствует какая-либо информация об объектах i-го класса.
Априорную вероятность можно оценивать различными способами. В случае репрезентативной выборки в качестве оценок априорных вероятностей можно использовать доли объектов в каждом классе. Например, если объем выборки составляет 1000 наблюдений, причем 600 (60%) наблюдений принадлежат к классу 1, а 400 (40%) — к классу 2, тогда априорная вероятность класса 1 равна 0,6, а класса 2 — соответственно 0,4.
В то же время маркетологу часто требуется заранее сконструировать выборку, чтобы в ней присутствовало заранее определенное число наблюдений. Такие задачи возникают, например, при проведении директ-маркетинга: число потребителей, ответивших на рассылку, составляет обычно небольшой процент от числа всех охваченных этой рассылкой. В связи с этим даже в достаточно большую выборку попадет немного информации об ответивших и маркетолог предпочтет включить в анализ одинаковое число ответивших и не ответивших потребителей. В этом случае вероятность принадлежности к классу не может быть оценена по описанному выше способу, ее нужно оценивать по каким-либо иным правилам (прошлому опыту, изучению накопленной статистики и т.п.).
Если исследователь не имеет вообще никакой информации о вероятностях и попадание во все группы равновероятно, априорные вероятности можно просто считать равными друг другу (для случая двух классов вероятности будут равны 0,5). Каждое из наблюдений должно принадлежать к какой-либо группе, поэтому сумма априорных вероятностей равна 1.
Априорные вероятности содержат некоторую информацию о вероятности принадлежности к определенной группе, но не учитывают особенности каждого отдельного наблюдения. Для того чтобы учесть эти особенности, необходимо оценивать вероятности с учетом дополнительных сведений о наблюдении. В том случае, например, если значения дискриминантной функции в каждом из двух классов имеют нормальное распределение и исследователь может оценить параметры этих распределений, можно рассчитать вероятность того, что дискриминантная функция примет значение D при условии принадлежности к классу 1 и аналогично рассчитать вероятность для класса 2. Каждая из этих вероятностей будет называться условной вероятностью значения D для данного класса и обозначается как P(D|Gi). При вычислении этой вероятности сначала предполагается, что наблюдения принадлежат к группе G1 и оценивается вероятность появления показателя, равного D. Затем предполагается, что наблюдения принадлежат к группе G2 и вычисления повторяются.
Условная вероятность значения D для данного класса показывает, насколько вероятно для членов класса получение именно этого значения. Но принадлежность наблюдения к тому или иному классу неизвестна, поэтому исследователь должен также оценивать вероятности принадлежности наблюдения к каждому из рассматриваемых классов (если известно, что значение индикатора для него равно D). Эта вероятность носит название апостериорной вероятности и обозначается как P(Gi|D). Эта вероятность может быть оценена с помощью правила Байеса с использованием вероятностей P(D|Gi) и P(Gi). Апостериорная вероятность задает оптимальное правило классификации: наблюдение следует отнести к тому классу, для которого апостериорная вероятность D максимальна.
Как и все методы математической статистики, дискриминантный анализ связан с целым рядом ограничивающих предположений [4]:
- предикторы должны быть измерены в числовой шкале — интервальной или относительной. Практика показывает, что метод может работать и с порядковыми переменными, но число градаций должно быть не слишком мало (не менее 5);
- каждому классу должно соответствовать многомерное нормальное распределение. При использования метода для решения практических задач это предположение часто нарушается, особенно при больших объемах выборок, что может привести к неточным оценкам значимостей и вероятностей принадлежности к классам. Но, как показывает практика, если классы достаточно хорошо разделимы, это не сказывается на работе решающего правила;
- матрицы ковариаций в разных классах должны быть равными. Когда это предположение нарушается, линейная разделимость не слишком удобна — известно, что в этом случае больше подходят квадратичные дискриминаторы. Но если различие матриц ковариаций не слишком велико и малы объемы выборок, линейные функции все-таки достаточно хорошо аппроксимируют решение.
Нарушение ограничивающих предположений увеличивает ошибку оптимального решающего правила!
Итак, при использовании дискриминантного анализа рекомендуется:
- иметь объем выборки, в 10-20 раз превышающий число предикторов;
- количество объектов каждого класса должно превышать число предикторов (эмпирическое правило — не менее, чем в 5 раз);
- конечная модель, как правило, не должна включать более 10 предикторов;
- необходимо проводить дополнительные исследования выбросов, которые могут негативно влиять на результат. Возможно проведение анализа с исключением выбросов.
- требуется принимать во внимание случаи, когда две переменные сильно коррелированы, хотя качество решающего правила при этом обычно не ухудшается.
В настоящей статье кратко описан лишь один из наиболее известных, часто применяемых методов математической статистики, основанных на откликах. В следующей статье предполагается рассмотреть метод логистической регрессии.
[1] Вообще говоря, для логистической регрессии это чрезмерно строгое утверждение.
[2] На практике такое условие выполняется крайне редко. Но многочис-ленные исследования показали, что условие многомерной нормальности не является критическим для эффективного применения дискриминант-ного анализа.
[3] Метод предложен Р.Фишером и соответствующие функции называются линейными дискриминантными функциями Фишера или просто фишеровскими классификаторами.
[4] Правда, специалисты в области математической статистики на основе практического опыта утверждают, что как этот метод, так и большинство статистических методов достаточно устойчивы к нарушениям этих предположений.

Комментарий
Новое сообщение