Практические вопросы рыночного сегментирования

Статья
комментарий

Сегментирование рынка является одним из важнейших, основополагающих элементов концепции маркетинга. Существует множество определений, в том числе и в авторитетных словарях по маркетингу.

«Сегментация рынка (market segmentation) — разделение рынка на четкие группы покупателей, которые могут предъявлять требования на разные продукты и специальные маркетинговые подходы. В результате сегментации определяются сегменты рынка. В зависимости от используемых критериев выделяют географическую, демографическую, психографическую и поведенческую сегментации. Указанные критерии используются при сегментировании рынка как потребительских товаров и услуг, так и продукции производственного назначения. Так, критериями сегментации (сегментирования) рынка потребительских товаров являются уровень доходов, место проживания, семейное положение, половозрастные и национальные характеристики. В производственной сфере в качестве критериев сегментации используются отраслевая принадлежность предприятия, его размеры, тип производства и характер энергопотребления. Сегментирование рынка может осуществляться на основе только одного критерия, а также на последовательном применении нескольких критериев. Важно, чтобы в последнем случае сегменты не оказались слишком малочисленными, невыгодными для коммерческого освоения. Сегментирование рынка может осуществляться на основе только одного критерия, а также на последовательном применении нескольких критериев».

При использовании этого достаточно исчерпывающего определения либо других подобных определений, а также при изучении соответствующих источников необходимо обратить внимание на то, что в более ранних переводах работ западных специалистов по маркетингу термин «segmentation» переводился как «сегментация»; в настоящее же время переводчики и редакторы считают более правильным перевод «сегментирование», который и используется в изданиях, выходящих в последние годы. Тем не менее эта небольшая терминологическая разница совершенно не влияет на суть рассматриваемого вопроса.

Необходимо подчеркнуть, что сегментирование является не единовременным актом, но динамическим, развивающимся процессом. Потребности потребителей постоянно развиваются и изменяются, поэтому компаниям периодически требуется пересматривать свои стратегии сегментирования, проводить переоценку рыночных сегментов. На практике для этого используются методы математической статистики, применение которых в настоящее время связано с использованием широко известных статистических пакетов. Материалы данной статьи связаны с использованием пакета SPSS.

Методы математической статистики, используемые при сегментировании

Кластерный анализ

Кластерный анализ является одним из наиболее известных, «классических» методов математической статистики, использующихся для сегментирования потребителей. Он представляет собой метод разведочного анализа, созданный для выявления областей концентраций в данных по какому-либо признаку.

В основе кластерного анализа лежит концепция распределения наблюдаемых данных по однородным группам в зависимости от их сходства («близости») друг с другом. В зависимости от разного понимания этой «близости» созданы различные методы кластерного анализа, наиболее распространенные из которых будут рассмотрены в данном параграфе. Здесь также приводится обзор типов данных, которые используются для кластеризации, и ряд практических аспектов сегментирования.

Кластерный анализ является одним из методов разведочного анализа данных, созданных для выявления каких-либо возможных группировок во всей совокупности данных. Основным критерием для объединения данных в группы является расстояние: объекты, расположенные «близко» друг к другу, должны попадать в один и тот же кластер, тогда как «достаточно далекие» объекты должны быть в разных кластерных группах. В идеальном случае все объекты внутри кластера должны быть достаточно однородными, но значительно отличаться от объектов из других кластеров. Поскольку кластерный анализ основан на расстояниях, измеренных в той же шкале, что и сами наблюдения, показатели близости можно рассматривать, как интервальные или порядковые. Результатом успешно проведенной кластеризации является выделение ряда сегментов внутри общего набора данных.

При использовании кластерного анализа для сегментирования потребителей необходимо помнить о том, что данный метод является разведочным. Соответственно, при его использовании нельзя ожидать получения единственного и определенного решения. На практике приходится иметь дело с несколькими решениями, и задача исследователя — выбрать среди них наиболее подходящее. Различные методы кластеризации (и нормировки) предлагают несколько различающиеся решения, и здесь уже от исследователя требуется глубже понять структуру данных.

При проведении кластеризации необходимо обращать внимание на следующие важные моменты:

разделение между группами — насколько значимым является различие между группами, разделены ли одни группы более, чем другие;
каково число наблюдений в каждой из групп (поскольку наличие выбросов в наблюдениях может привести к формированию кластеров, содержащих одно-два наблюдения);
средние значения кластерных групп, вычисленных по кластерным переменным (наиболее наглядно эти средние значения можно наблюдать на графиках, которые помогут также при интерпретации и именовании кластеров);
верификация, т. е. определение, имеют ли полученные кластеры какой-либо содержательный смысл, воспроизводятся ли они для разных выборок и при использовании различных методов кластеризации.

Как было показано выше, основной целью при проведении кластерного анализа является выделение естественно возникающих групп на основе их схожести. Но при практическом применении конкретных методов появляются отличия, связанные с различными способами вычисления расстояния между двумя наблюдениями (или кластерами) и с правилами, используемыми для формирования кластеров. Поэтому исследователь может применять разнообразные методы кластерного анализа, наиболее популярные из них будут рассмотрены в данном параграфе. Каждый метод, разумеется, не идеален и имеет свои достоинства и недостатки, которые необходимо учитывать при проведении кластеризации.

Одним из основных различий является различие между иерархическими и неиерархическими методами.

При иерархической кластеризации объекты (отдельные наблюдения или кластеры), попавшие в кластер, остаются объединенными на всех последующих этапах кластеризации. Методы различаются по способам оценки расстояния между кластерами.

Рисунок 1 иллюстрирует простое решение методом иерархической кластеризации. Объекты В и Е являются наиболее близкими друг к другу и формируют кластер. При слиянии этого кластера с объектом А в новый кластер будут включены оба объекта: как В, так и Е. Это свойство, т. е. сохранение в одном кластере уже однажды присоединенных объектов, является определяющим для иерархической кластеризации.

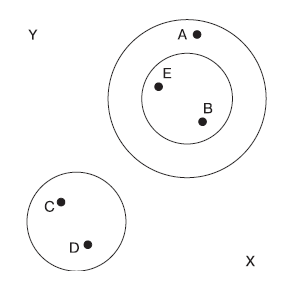
Рис. 1. Иерархическая кластеризация

Неиерархические методы не требуют, чтобы попавшие в кластер объекты оставались в этом же кластере в течение всего дальнейшего процесса кластеризации. Одним из наиболее распространенных методов неиерархической кластеризации является алгоритм k-средних. При его использовании исследователь должен предварительно задать требуемое число кластеров (k), и работа алгоритма приведет к созданию из данных именно заданного числа кластеров. Число кластеров подбирается экспериментально: как правило, предпринимается несколько попыток кластеризации с разным числом кластеров, и затем результаты сравниваются, и выбирается окончательное решение (могут использоваться упомянутые выше критерии — число наблюдений на группу, профили средних, верификация).

Иерархические методы

Итак, иерархические методы кластеризации различаются между собой по способам оценки расстояния между кластерами (их «близости») при формировании кластеров. Например, если есть два кластера, содержащие по два объекта в каждом, то:

в случае, если под этим понимается расстояние между центрами тяжести кластеров, имеет место метод «центроида» (или средних значений);
если понимается кратчайшее возможное попарное расстояние между точками из разных кластеров — метод «ближайших соседей» (называемый также методом простого связывания);
если наоборот — понимается наибольшее попарное расстояние между точками, речь идет о кластеризации методом «самого далекого соседа» (или полного связывания);
если вместо центров тяжести кластеров используются медианы, то приходим к методу медианного связывания.

Если исследователь предпочитает явным образом включать в вычисление расстояния все объекты из кластера, он может остановиться на методе межгруппового среднего связывания (называемом также невзвешенным попарно-групповым методом с использованием арифметических средних — английская аббревиатура UPGMA), при котором расстояние оценивается для всех возможных пар наблюдений из двух разных кластеров и затем берется среднее значение. С другой стороны, метод Варда создает кластеры, комбинируя те из них, которые приводят к наименьшим внутрикластерным суммам квадратов.

Приведенные ниже рисунки иллюстрируют на простых примерах, как некоторые из методов определяют расстояние между двумя кластерами (рис. 2 — 5).

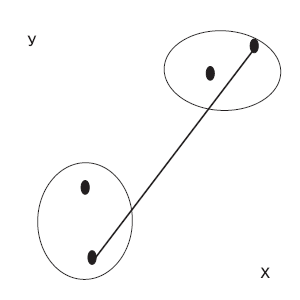
Рис. 2. Метод ближайшего соседа (простого связывания)

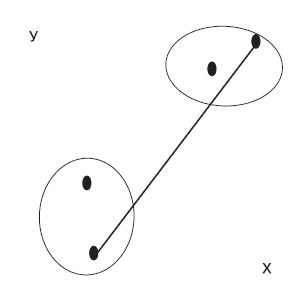
Рис. 3. Метод самого дальнего соседа (полного связывания)

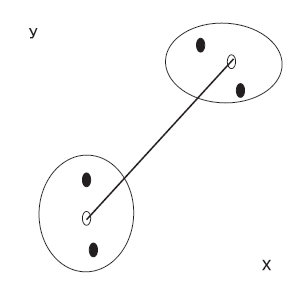
Рис. 4. Метод центроида

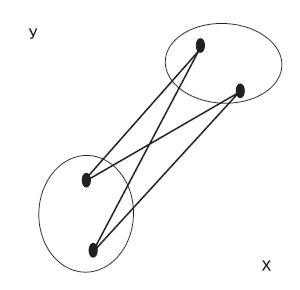
Рис. 5. Метод межгруппового среднего связывания

К сожалению, среди описанных методов невозможно выделить какой-либо «наилучший», одинаково хорошо работающий для любых типов данных. В каждом конкретном случае задача выбора того или иного метода должна решаться исследователем исходя из собственного опыта, характера имеющихся данных и с учетом ряда приводимых ниже эмпирических рекомендаций.

Специалисты, имеющие опыт работы с иерархическими методами, выделяют некоторые характеристики, помогающие исследователю выбирать в каждом случае наиболее подходящий метод:

Метод ближайшего соседа (простого связывания)

Тяготеет к созданию удлиненных, «колбасообразных» кластеров, вытягивающихся за счет присоединения ближайшей точки.
Менее чувствителен к выбросам.

Кроме того, метод связан с некоторыми замечательными формальными математическими свойствами, которые, правда, не имеют существенного практического значения.

Метод самого дальнего соседа (полного связывания)

Менее чувствителен к выбросам.

Метод центроида

Работает лучше на «засоренных» данных.
Менее чувствителен к выбросам.

Метод межгруппового среднего связывания

Работает лучше на «засоренных» данных.
Чувствителен к выбросам.
По мнению специалистов, работает хорошо при разнообразных условиях.
Возможно образование кластеров со схожими дисперсиями.

Метод Варда

Работает лучше на «засоренных» данных.
Чувствителен к выбросам.
Возможно образование кластеров со схожими размерами.

Ни один из этих методов не превосходит остальные, каждый имеет свои достоинства и недостатки. Основываясь на исследованиях методом Монте-Карло и эмпирических соображениях, специалисты утверждают, что методы межгруппового среднего связывания, Варда и самого дальнего соседа предпочтительнее остальных. Тем не менее это лишь самая общая рекомендация, и для некоторых специфических структур данных (или проблем) может понадобиться метод, более чувствительный (или устойчивый).

Неиерархические методы

Как было упомянуто выше, неиерархические методы кластеризации не требуют, чтобы два объекта, попавшие в один и тот же кластер, оставались там и впоследствии. Таким образом, они накладывают менее строгие ограничения на структуру данных, чем иерархические методы. Самой популярной техникой в этом классе методов является метод (или алгоритм) k-средних. Буква «k’» в названии метода связана с тем, что при каждом обращении к методу исследователь должен сам выбирать (предлагать) число (k) образуемых кластеров. Слово «средних « в названии связано с тем фактом, что каждый кластер определяется средним значением (или центром тяжести) своих объектов.

Поскольку для работы метода k-средних исследователю необходимо указать определенное число кластеров, то, как правило, производится несколько попыток с разным числом кластеров, а полученные результаты оцениваются при помощи различных критериев (сепарации, размера групп, рисунка средних и верификации). Т. к. число кластеров выбирается заранее, и оно обычно мало по сравнению с общим числом объектов, метод k-средних работает намного быстрее, чем иерархические методы. Это происходит потому, что если задано, например, семь кластеров для анализа, то при работе метода требуется отследить только семь кластеров. В иерархической же кластеризации на каждом шаге необходимо оценивать попарное расстояние для каждой пары объектов и пересчитывать межкластерные расстояния (что является достаточно интенсивной вычислительной задачей). Таким образом, для выполнения кластерного анализа на большом количестве объектов (много сотен или тысяч) обычно выбирают метод k-средних (хотя исследователь может сделать и сравнительно небольшую выборку из большого файла данных и применить иерархический метод).

С другой стороны, в ряде случаев для исследователя может быть даже удобным то, что он может проверить свои собственные идеи (или применить результаты других исследований) при задании кластеров. В SPSS, например, существует специальный режим, при котором можно задать начальные значения для каждого из кластеров, и процедура k-средних будет отталкиваться в своем анализе от них.

Если же не заданы стартовые значения для средних k кластеров, файл данных просматривается в поисках k достаточно удаленных друг от друга (в смысле расстояний, основанных на наборе кластерных переменных) объектов, которые будут использованы как исходные центры кластеров. Затем файл данных повторно считывается, при этом каждый объект относится к своему ближайшему кластеру. В завершение каждая точка попадает в какой-нибудь кластер, а средние значения (центры тяжести) кластеров обновляются с учетом добавленных объектов (по решению исследователя обновление может происходить после каждого включения какого-либо объекта в кластер). По меньшей мере один дополнительный итерационный шаг (исследователь может контролировать число итераций) совершается для того, чтобы проверить, остается ли каждый объект по-прежнему ближайшим к центру тяжести своего собственного кластера (поскольку центры кластеров могут сдвигаться при их обновлении после добавления или удаления объектов), и если нет — данный объект попадает в ближайший к нему на данный момент кластер. Дополнительные шаги и могут повторяться, пока не останется объектов, переходящих из одного кластера в другой.

Из практики применения метода известно, что кластеризация методом k-средних эффективна, когда центры тяжести исходных кластеров достаточно удалены друг от друга; кроме того, на больших файлах метод работает гораздо быстрее иерархических методов. Правда, следует принять во внимание следующее:

прежде чем остановиться на каком-либо решении, требуется, как правило, произвести несколько попыток;
поскольку этот метод неиерархический, для него нельзя построить дендрограмму, весьма полезную при оценивании кластерных решений.

Таким образом, для не очень больших файлов данных (содержащих не более нескольких сотен и особенно менее ста наблюдений) некоторые иерархические методы (полного связывания, межгруппового среднего связывания, Варда) работают очень хорошо, и результаты можно представить в виде дендрограммы. Для больших файлов (много сотен или тысяч наблюдений) наиболее эффективным, а с точки зрения системных ресурсов единственно возможным методом будет алгоритм k-средних. Хоти и метод межгруппового среднего связывания, и метод Варда чувствительны к выбросам, эту проблему можно решить, по крайне мере отчасти, удалив наблюдения, формирующие единичные (или очень маленькие) кластеры из файла данных и повторно проведя кластерный анализ.

Расстояние и нормировка

Помимо различных методов кластеризации, необходимо также принимать во внимание существование множества различных техник измерения расстояния между объектами. На рисунках 2 и 3 расстояние между двумя объектами представлено в виде прямой линии или евклидова расстояния. Если в кластеризации участвуют две переменные X (x₁, y₁) и Y (x₂,y₂), то да евклидово расстояние между ними будет равно:

Евклидово расстояние, вычисленное таким способом, интуитивно понятно, но на практике чаще используется квадрат евклидова расстояния, что усиливает роль больших расстояний и лучше согласуется с показателями сумм квадратов, применяющимися во многих статистических процедурах.

Существует другой способ измерения расстояний, называемый метрикой «городского квартала» (рис. 6).

Рис. 6. Расстояние «городского квартала»

Вычисление расстояния «городского квартала» между двумя объектами заключается во взятии модуля разности между ними по каждому измерению, а затем в суммировании этих разностей. Название метрики интерпретируется достаточно просто: если бы два объекта были зданиями в городе, то путь от одного к другому пролегал бы вдоль городских кварталов, пересекающихся под прямым углом (что отличает эту метрику от прямого кратчайшего маршрута, представляющего евклидову метрику).

Данная метрика удобна, например, в том случае, когда исследователю необходимо вычислять расстояние между двумя потребителями как сумму того, насколько они различаются по каждому заданному им измерению, — в этом случае следует воспользоваться именно расстоянием «городского квартала». Однако на практике оно используется все же не так часто, как евклидово расстояние.

При использовании методов кластеризации применяется и множество других метрик (расстояний) — в частности, разнообразные варианты расстояний, если кластеризуемые переменные представляют собой подсчеты (например, частоту приобретения или использования разных изделий). Если данные являются двузначными (если потребители представлены перечнем вопросов, прилагаемым к изделию или перечнем используемых ими свойств этого изделия), могут использоваться двузначные метрики. Двузначная метрика Ланса и Уильямса сочтет потребителей схожими, если они оба пометят какой-нибудь раздел в каталоге или опросном листе, и несхожими — если этот раздел не пометит ни один из них.

Рассмотренные выше метрики расстояний не учитывают каким бы то ни было образом корреляций, возможно, существующих между кластеризуемыми переменными. Поэтому происходит следующее: если две переменных сильно коррелированы друг с другом, то их совместное использование в кластерном анализе значительно увеличивает их вес при вычислении различных показателей. При коэффициенте корреляции, равном единице (в случае линейной пирсоновской корреляции), это эквивалентно двойному зачету одной и той же переменной. Это одна из реальных проблем, возникающих при кластерном анализе данных, описывающих большое количество атрибутов какого-либо изделия. Возможным решением этой проблемы будет предварительное проведение факторного анализа, а затем кластерного анализа уже факторизованных данных (факторный анализ будет рассматриваться в следующем параграфе данной главы).

Помимо этого, для того чтобы вычислять расстояния, все кластеризуемые переменные должны быть комплектными (не иметь пропущенных значений). Иерархические методы требуют полностью определенных данных, в то время как алгоритм k-средних имеет возможность, допускающую использование данных с пропущенными значениями. Поэтому если в данных много пропущенных значений, необходимо либо исключить из анализа переменные с высокой концентрацией пропущенных значений, либо использовать метод k-средних.

Итак, по поводу применения метрик можно сделать следующий вывод: исследователь может пользоваться различными метриками, но, как показывает практика, большее влияние на решение оказывает выбор метода кластеризации, а не способ вычисления расстояний.

Нормировка кластеризуемых переменных

При использовании методов кластерного анализа исследователь должен также принять решение о том, надо ли нормировать тем или иным способом кластеризуемые переменные.

Если у исследуемых переменных совершенно разный масштаб, то нормировка обычно производится для того, чтобы устранить слишком сильное влияние одной из переменных на расстояние между ними. Нормировка производится при помощи так называемых z-вкладов, что позволяет каждой переменной получить одинаковое стандартное отклонение.

Но в то же время нормировка может уменьшить влияние важных кластеризуемых переменных (из-за сжатия их масштаба), и по этой причине она не должна производиться автоматически, только если анализируются переменные с разным масштабом или с одинаковым масштабом, но с разными стандартными отклонениями. Наиболее часто используется нормировка каждой переменной к форме z-вклада (нулевое среднее значение и единичное стандартное отклонение): кластеры с положительным средним вкладом расположены над общим средним значением, с отрицательным вкладом — под ним, и их величину можно интерпретировать в единицах стандартных отклонений.

Существуют и другие способы нормировки: переменные можно нормировать к интервалу [-1,+1], или к единичному интервалу [0, 1], или так, чтобы максимальное значение было равно 1 и т. д. Если необходимо выполнить нормировку, это можно сделать как в рамках каждой переменной, так и каждого наблюдения. Нормировка для каждого наблюдения (или обоими способами) означает, что исследователя в большей степени интересует кластеризация, основывающаяся на сходстве профилей кластеризуемых переменных, нежели чем на собственно расстояниях (графики профилей средних значений хорошо иллюстрируют это утверждение).

Основные рекомендации при проведении кластерного анализа:

в исследованиях, связанных с кластерным анализом, использование квадрата евклидова расстояния является наиболее распространенным;
при кластеризации переменных с совершенно разными масштабами, обычно производится их нормировка того или иного типа (как правило, приведение к z-вкладам);
для кластеризации по схожим тенденциям откликов (а не по разностям в их значениях) наиболее подходящими типами нормировок являются нормировка по каждому наблюдению (объекту) или нормировка обеими способами;
выбранный метод кластеризации влияет на решение в большей степени, чем выбранная метрика (способ вычисления расстояния);
если масштаб (величина стандартного отклонения) сильно варьируется от переменной к переменной, то нормировка может значительно повлиять на результат.

Итак, выше были рассмотрены как общие принципы кластерного анализа, так и особенности его использования для сегментирования, а также предложен ряд практических рекомендаций по работе с процедурой кластерного анализа.

Виктор Гречков

Комментарий

Новое сообщение

Статья
комментарий

Авторизация